Kaplan

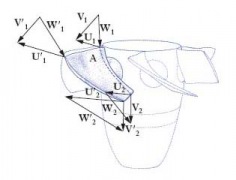
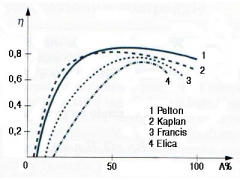
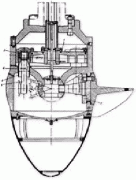
Quando una turbina Francis di media/grande potenza è destinata ad operare sotto un salto basso, supponiamo 15 m, tipico di installazioni su grandi fiumi, la portata dovrebbe essere di almeno 150 m3/s per ottenere una Potenza attorno ai 20 MW avendo assunto un rendimento µ = 93%. Variazioni di salto per es. del 15% fra min e max sono tipici delle turbine Francis anche se ci sono casi con variazioni ben più significative. Quando una centrale è posta su un fiume le variazioni di salto sono ben più del 15% attestandosi mediamente attorno al 50%. Tali variazioni influiscono notevolmente sul buon funzionamento di una Francis mentre son ben tollerate dalle Kaplan che hanno la possibilità di usufruire di una doppia regolazione tramite le direttrici, come nelle Francis, in sincronia con le pale ruota che ruotano attorno a perni alloggiati nel mozzo (fig 3) tramite meccanismi biella-manovella, comandati a loro volta da un servomotore alloggiato nello stesso mozzo o ricavato fra gli accoppiamenti degli alberi. La possibilità della doppia regolazione consente di avere delle curve di rendimento più estese rispetto alle Francis e alle eliche (Kaplan con pale fisse) (fig 2), poiché le pale vengono ad assumere la posizione più opportuna in ragione del mutare dei triangoli di velocità (fig 1).

Fig 1

Fig 2

Fig 3


La turbina Kaplan si impiega normalmente nel campo 95< nq <275
indichiamo con K il coefficiente di velocità periferica il cui campo di variazione è fra 1,25< k<2,5. Assumendo n11= 84,5 K (la dimostrazione andrebbe oltre lo scopo di questa sintesi) potremo scrivere 105<n11<210 ed utilizzando la tabella sottostante determinare il diametro della ruota e altre grandezze caratteristiche della turbina.

nq
95
110
125
135
150
165
180
190
205
220
230
245
260
275
K
1,24
1,31
1,39
1,48
1,56
1,65
1,75
1,85
1,94
2,04
2,14
2,25
2,36
2,48
n11
104
110
116
123
130
137
145
154
162
170
178
187
197
207
\bf\Large\frac { B }{ { D }_{ e } }
0,36
0,365
0,372
0,38
0,386
0,392
0,4
0,406
0,412
0,42
0,426
0,432
0,44
0,45
\bf\Large\frac { { Z }_{ d }{\LARGE a }_{ 0 } }{ { D }_{ e }}
1,7
1,84
2
2,12
2,26
2,38
2,5
2,6
2,7
2,8
2,88
2,95
3,04
3,1
 


ESEMPIO

Siano dati i seguenti valori:  H = 30 m    Q = 400 m3/s    n = 94,74 rpm ( f= 60 Hz)

Per turbine così grandi è lecito aspettarsi rendimenti elevati e nel nostro caso assumiamo µ = 94%. La potenza all’ asse turbina sarà: N= 110650 Kw (Fondamenti [a]) nq=150 (Fondamenti [b]) e dalla tabella si ricava n11= 130. Ricordando che:

n11=\bf\frac {{\large n}D}{\sqrt { H}} (Fondamenti)   si ricava D= 7,5 m.

Usufruendo ancora della tabella:
B/De = 0,386 e quindi B = 2,9 m (fig 4). Ancora zda0/De = 2,26 e con zd=24 (N.direttrici) a0=0,7 m apertura fra le direttrici ( Francis ) (fig 4). In genere il mozzo può essere assunto pari a 0,45D, dipendendo dal numero delle pale ruota e dalle sollecitazioni a cui è sottoposto. Sotto il salto di 30 m può essere adottata una ruota a 5 pale e il diametro del mozzo sarà approssimativamente Dm= 3,4 m.

Gallery

Fig 4

Fig 5

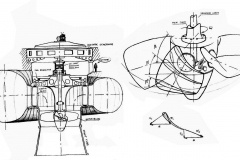
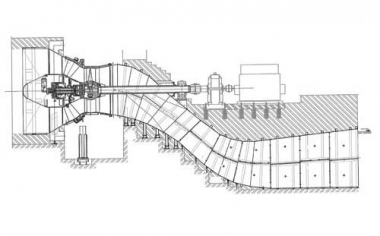
Fra le turbine Kaplan possiamo annoverare le turbine ad S. Sono chiamate in questo modo per la tipologia dello scarico. Sono caratterizzate da bassi salti e portate relativamente grandi. I bassi salti impongono quindi una disposizione orizzontale.

Fig 6

In fig 6 è rappresentata una turbina di questo tipo avente le seguenti caratteristiche:
Salto netto…………………….. 9 m
Portata max…………………… 40 m3/s
Potenza all’asse turbina …. 3,27 MW
Velocità nominale turbina… 150 rpm
Velocità generatore………… 750 rpm

Osservando la figura si nota il distributore conico, la ruota tipo Kaplan, all’uscita dell’albero motore dallo scarico il supporto, quindi un giunto snodabile per compensare eventuali disallineamenti, il moltiplicatore di giri che porta la rotazione turbina da 150 a 750 rpm e il generatore stesso. Se non ci fosse stato il moltiplicatore di giri le dimensioni del generatore sarebbero state molto più grandi.